Предметом главы в целом является изучение слабо связанных последовательных
процессов. Данный раздел посвящен тщательному рассмотрению простой, но
характерной задачи, на примере которой читатель познакомится с возникающими в
этой области проблемами.
В предыдущем разделе мы описали природу изолированного последовательного
процесса, в котором последовательность действий выполняется автономно, т.е.
независимо от окружающей обстановки.
Если двум или более последовательным процессам необходимо взаимодействовать
друг с другом, то они должны быть связаны, т. е. иметь средства для обмена
информацией. Как мы увидим ниже, свойства таких средств связи играют важную
роль.
Кроме того, мы предполагаем, что процессы связаны слабо. Под этим
подразумевается, что кроме (достаточно редких) моментов явной связи, эти
отдельные процессы рассматриваются как совершенно независимые друг от друга. В
частности, не допускаются какие-либо предположения об относительных скоростях
различных процессов. (Скажем, такое предположение, как "процессы
синхронизированы относительно некоторого общего времени", может рассматриваться
как неявная связь.) Независимость от соотношения скоростей полностью
соответствует нашему определению последовательного процесса, единственным
существенным свойством которого является то, что элементарные шаги процесса
выполняются последовательно. Если нужно, мы можем следить по часам за
выполнением процесса, но сам он от этого совершенно не зависит.
Отказ от каких-либо предположений о соотношении скоростей на первый взгляд
покажется читателю неоправданной попыткой представить вещи в более сложном виде,
чем они есть на самом деле. Однако это полностью обосновано. Во-первых, нам,
возможно, придется иметь дело с ситуациями, в которых действительно мало что
известно о скоростях. Например, одной частью системы может быть управляемая
вручную станция, а другая часть системы характеризуется тем, что она может
останавливаться по внешнему воздействию на неопределенное время, тем самым
уменьшая скорость "выполнения" процесса до нуля. Во-вторых, - и это значительно
более важно, - когда мы думаем, что можем полагаться на некоторое соотношение
скоростей, то оказывается в конце концов, что мы погнались за пенни, а упустили
фунт. Конечно, отдельные устройства можно сделать проще в предположении
ограничений на их скорости. Однако задача создания надежной работоспособной
системы из многих связанных элементов значительно усложняется, если необходимо
учитывать их взаимное влияние друг на друга и согласовывать скорости. (Прежде
всего это создает весьма неустойчивое равновесие в работе, чувствительное к
любым изменениям скоростей, которые легко возникают при замене элементов
системы, скажем, при установке более быстрой модели построчного печатающего
устройства или при перепрограммировании какой-либо части программного
обеспечения.)
2.1. Простой пример
Рассмотрим два последовательных процесса: "процесс 1" и "процесс 2", которые
для наших целей удобно считать циклическими. В каждом цикле выполнения процесса
существует "критический интервал", критический в том смысле, что в любой момент
времени только один из процессов может находиться внутри своего критического
интервала. Чтобы осуществить такое "взаимное исключение", оба процесса имеют
доступ к некоторому числу общих переменных. Мы постулируем, что проверка
текущего значения такой общей переменной и присваивание нового значения общей
переменной рассматриваются как неделимые, не допускающие вмешательства действия;
то есть, если два процесса осуществляют присваивание нового значения одной и той
же общей переменной "одновременно", то присваивания происходят друг за другом и
окончательное значение переменной соответствует одному из присвоенных значений,
но никогда не есть их "смесь".
Подобно этому, если один процесс проверяет значение переменной "одновременно"
с присваиванием ей значения другим процессом, то первый обнаруживает либо
старое, либо новое значение, но никогда не их смесь.
Для наших целей АЛГОЛ-60 не подходит, так как он создан для описания
единственного последовательного процесса. Поэтому /мы используем некоторое его
расширение, позволяющее описывать параллельное выполнение. Если
последовательность операторов - как обычно разделенных точкой с запятой -
заключена в специальные операторные скобки "parbegin" и
"parend", то это интерпретируется как параллельное
выполнение составляющих конструкцию операторов. Вся конструкция - назовем ее
"параллельный блок" - может рассматриваться как оператор. Запуск параллельного
блока означает одновременный запуск всех составляющих его операторов; выполнение
блока завершается после завершения выполнения всех составляющих его операторов.
Например,
begin S1; parbegin S2; S3; S4; parend; S5 end
(где S1, S2, S3, S4 и
S5 есть операторы) означает, что после завершения S1,
операторы S2, S3 и S4 будут выполняться
параллельно, и только после того, как все они завершатся, начнется выполнение
оператора S5.
Теперь при определенных выше соглашениях об использовании общих переменных мы
можем написать первое решение проблемы взаимного исключения:
begin integer очередь; очередь := 1;
parbegin
процесс 1: begin L1: if очередь = 2 then goto L1;
критический интервал 1;
очередь := 2;
остаток цикла 1; goto L1
end;
процесс 2: begin L2: if очередь = 1 then goto L2;
критический интервал 2;
очередь := 1;
остаток цикла 2; goto L2
end;
parend
end
(Сделаем замечание для читателя, недостаточно знакомого с языком АЛГОЛ-60.
После "begin" в первой строке стоит так называемое описание
"integer очередь", ибо, согласно правилам языка АЛГОЛ-60 в
тексте программы нельзя ссылаться на переменные, не введенные с помощью
описания. Так как это описание располагается после "begin",
являющегося самой внешней операторной скобкой, то это означает, что на время
выполнения всей программы введена переменная, которая будет принимать только
целые значения, и к которой можно обратиться с помощью имени
"очередь".)
Два процесса связываются друг с другом через общую целочисленную переменную
"очередь", значение которой показывает, какой из двух процессов
первым выполнит (точнее, закончит) свой критический интервал. Из программы ясно,
что после первоначального присваивания единственными возможными значениями
переменной "очередь" являются "1" и "2".
Условием входа в критический интервал для процесса 2 является "очередь
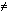 1", т. е. "очередь = 2". Но
единственный способ для переменной "очередь" получить это значение
есть присваивание "очередь := 2" в процессе 1. Так как процесс 1
выполняет это присваивание только по завершении своего критического интервала,
то процесс 2 может войти в свой критический интервал только после завершения
критического интервала 1. А критический интервал 1 действительно мог быть
выполнен, потому что начальное условие "очередь = 1" означает
одновременно "очередь
1", т. е. "очередь = 2". Но
единственный способ для переменной "очередь" получить это значение
есть присваивание "очередь := 2" в процессе 1. Так как процесс 1
выполняет это присваивание только по завершении своего критического интервала,
то процесс 2 может войти в свой критический интервал только после завершения
критического интервала 1. А критический интервал 1 действительно мог быть
выполнен, потому что начальное условие "очередь = 1" означает
одновременно "очередь 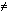 2", и значит
потенциальный цикл ожидания, помеченный в программе как L1,
первоначально бездействует. После присваивания "очередь := 2" роли
процессов меняются. {Замечание. Предполагается, что других ссылок на
переменную "очередь", кроме тех, которые явно присутствуют в
программе, не существует.)
2", и значит
потенциальный цикл ожидания, помеченный в программе как L1,
первоначально бездействует. После присваивания "очередь := 2" роли
процессов меняются. {Замечание. Предполагается, что других ссылок на
переменную "очередь", кроме тех, которые явно присутствуют в
программе, не существует.)
Наше решение, хотя и правильное, имеет, однако, излишнее ограничение: после
завершения критического интервала 1, переменная "очередь"
становится равной "2" и должна вновь получить значение
"1", чтобы разрешить следующий вход в критический интервал 1. Как
результат этого, единственно допустимая последовательность критических
интервалов представляет собой строгое их чередование "1, 2, 1, 2, 1, 2, 1,
... ", т. е. процессы синхронизированы. Для того, чтобы четко определить
нежелательность для нас подобного решения, мы поставим дополнительное условие:
"если один из процессов остановился вне своего критического интервала, то это не
должно привести к блокировке другого процесса" 1).
Поэтому предыдущее решение не приемлемо, и мы должны искать новое.
Наша вторая попытка связана с введением двух целочисленных переменных
"cl" и "с2", причем cl = 0 (или
1) или c2 = 0 (или 1) соответственно
будет означать, что процесс 1 или процесс 2 находятся внутри (или вне)
критического интервала. Предлагается следующее решение:
begin integer cl, c2;
cl := 1; c2 := 1;
parbegin
процесс 1: begin L1: if c2 = 0 then goto L1;
cl := 0;
критический интервал 1;
c1:= i;
остаток цикла 1; goto L1
end;
процесс 2: begin L2: if cl = 0 then goto L2;
c2 := 0;
критический интервал 2;
c2 := 0;
остаток цикла 2; goto L2
end;
parend;
end
Первоначальные присваивания устанавливают cl и c2 в
"1" в соответствии с тем фактом, что процессы начинают выполняться
вне своих критических интервалов. Во все время выполнения критического интервала
1 сохраняется соотношение "cl = 0" и потому первая строка в записи
процесса 2 представляет по существу ожидание: "ждать до тех пор, пока процесс 1
находится в своем критическом интервале." Такое решение проблемы действительно
отчасти предохраняет от одновременного выполнения критических интервалов, но
оно, к сожалению, потому слишком просто, что неверно. Пусть сначала процесс 1
обнаружит, что "c2 = 1".
Пусть процесс 2 немедленно вслед за этим проверяет значение cl;
тогда он еще найдет, что "cl = 1". Каждый из процессов,
удостоверившись, что другой не находится в критическом интервале, решит, что он
может безопасно войти в свой собственный критический интервал!
Мы должны действовать более осторожно. Давайте поменяем местами в самом
начале процессов проверку чужого "с" и установку собственного
"с". Получаем такую программу:
begin integer cA, c2;
cl := 1; c2 := 1;
parbegin
процесс 1: begin Al : cl := 0;
L1 : if c2 = 0 then goto L1;
критический интервал 1;
cl := 1;
остаток цикла 1; goto Al
end;
процесс 2: begin A2 : c2 := 0;
L2 : if cl = 0 then goto L2;
критический интервал 2;
c2 := 1;
остаток цикла 2; goto A2
end;
parend;
end
Имеет смысл убедиться в том, что это решение во всяком случае совершенно
безопасно. Давайте сосредоточим внимание на моменте, когда процесс 1
обнаруживает, что "c2 = 1", и поэтому решает войти в свой
критический интервал. В этот момент мы можем заключить:
- соотношение "cl = 0" уже установлено и будет сохраняться,
пока процесс 1 не завершит выполнение своего критического интервала;
- так как "c2 = 1", то процесс 2 находится вне критического
интервала, в который он не может войти, пока сохраняется "cl =
0", т. е. пока процесс 1 еще пребывает в своем критическом интервале.
Итак, взаимное исключение действительно гарантировано.
Но, увы, это решение также должно быть отвергнуто: предпринятые в нем меры
безопасности слишком сильны, так что оно содержит опасность взаимной блокировки.
Если после присваивания "cl := 0", но еще до проверки
c2 (и то, и другое в процессе 1), процесс 2 выполнит присваивание
"c2 := 0", то это значит, что оба процесса достигли соответственно
меток L1 и L2 и одновременно справедливы соотношения
"cl = 0" и "c2 = 0". В итоге процессы будут
безрезультатно ждать друг от друга разрешения войти в критический интервал.
Мы правильно поступили, установив собственное "с" до проверки
чужого "с", но неправильно было сохранять только состояние ожидания
с неизменным установленным собственным "с". Это до некоторой
степени исправлено в следующей конструкции:
begin integer cl, c2;
cl := 1; c2 := 1;
parbegin
процесс 1: begin L1: cl := 0;
if c2 = 0 then
begin cl := 1; goto L1 end;
критический интервал 1;
cl := 1;
остаток цикла 1; goto L1
end;
процесс 2: begin L2: c2 := 0;
if cl = 0 then
begin c2 := 1; goto L2 end;
критический интервал 2;
c2 := 1;
остаток цикла 2; goto L2
end;
parend;
end
Эта конструкция столь же безопасна, как и предыдущая, а если присваивания
"cl := 0" и "с2 := 0" выполняются "одновременно", то
это не приводит с неизбежностью к взаимной блокировке до бесконечности; дело в
том, что оба процесса установят свои собственные "с" обратно в
"1", прежде чем возобновить попытку входа в критический интервал,
тем самым предоставляя другому процессу возможность поймать удобный момент. Но
наши принципы заставляют отбросить также и это решение, так как отказ от
каких-либо предположений относительно соотношения скоростей означает, что
решение должно быть справедливым при любых скоростях, а последняя конструкция
позволяет так подобрать скорости, что процессы будут проверять чужие
"с" только в те моменты времени, когда значения их собственных
"с" нулевые. Чтобы четко определить неприемлемость таких решений,
которые работают только при некоторых удачных обстоятельствах, мы установим
следующее требование: "если два процесса находятся перед входом в свои
критические интервалы, то должно быть выполнено требование о невозможности
подобрать для них такие конечные скорости, при которых решение о том, какому из
них первому войти в свой критический интервал, откладывается до
бесконечности".
Между прочим, заметим, что отброшенное решение вполне приемлемо в
повседневной жизни. Например, когда два человека разговаривают по телефону и
связь неожиданно разъединяется, оба, как правило, пытаются восстановить связь.
Каждый из собеседников набирает номер и, если слышит сигнал "занято", то кладет
телефонную трубку. Если тут же не происходит вызов, то он делает вторую попытку,
спустя несколько секунд. Конечно, эта попытка может совпасть со следующей
попыткой партнера, но обычно связь восстанавливается после небольшого числа
проб. В наших условиях мы не можем принять такую схему поведения: у нас партнеры
могут быть совершенно идентичны.
Предлагалось довольно много решений этой задачи, и все они оказались
некорректными, так что у тех, кто занимался ею, возникло в какой-то момент
сомнение, имеет ли она решение вообще. Первое правильное решение принадлежит
голландскому математику Деккеру. Это решение представляет в действительности
некоторое объединение наших предыдущих попыток: в нем используются "переменные
безопасности", подобные тем, что обеспечивали взаимное исключение в последних
конструкциях, вместе с целочисленной переменной "очередь" первого
решения, но только для разрешения неопределенности, когда ни один из двух
процессов не продвигается немедленно в критический интервал. Отметим, что в
предлагаемой ниже программе начальное значение переменной "очередь"
может быть положено также и равным "2".
begin integer cl, c2, очередь;
cl := 1; c2 := 1; очередь := 1;
parbegin
процесс 1: begin Al: cl := 0;
L1: if c2 = 0 then
begin if очередь = 1 then goto L1;
cl := 1;
Bl: if очередь = 2 then goto Bl;
goto A1
end;
критический интервал 1;
очередь := 2; cl := 1;
остаток цикла 1; goto Al
end;
процесс 2: begin A2: c2 := 0;
L2: if cl = 0 then
begin if очередь = 2 then goto L2;
c2 = 1;
B2: if очередь = 1 then goto B2;
goto A2
end;
критический интервал 2;
очередь := 1; c2 := 1;
остаток цикла 2; goto A2
end;
parend;
end
Докажем теперь корректность этого решения. Во-первых, отметим, что каждый
процесс оперирует только с собственным "с".
Вследствие этого процесс 1 проверяет "c2" только при "cl =
0"; он войдет в свой критический интервал только тогда, когда обнаружит,
что "c2 = 1". Для процесса 2 можно сделать аналогичное замечание.
Короче говоря, мы узнаем переменные безопасности наших последних конструкций,
и поэтому решение безопасно в том смысле, что два процесса никогда не могут
оказаться одновременен) в своих критических интервалах.
Во второй части доказательства необходимо показать, что в случае сомнения,
какому из двух процессов первым войти в критический интервал, выяснение этого
вопроса не может откладываться до бесконечности. Теперь мы обратим внимание на
целочисленную переменную "очередь": замечаем, что присваивание
значения этой переменной происходит только при окончании критических интервалов
(или по окончании некоторых их частей), поэтому можно считать переменную
"очередь" константой во время принятия решения о том, кому войти в
критический интервал. Предположим, что "очередь = 1". Тогда процесс
1 может только циклиться через метку L1 (при этом "с1 =
0") и только до тех пор, пока он находит, что "с2 = 0". Но
если "очередь = 1", то процесс 2 может циклиться только через
В2, а это состояние процесса 2 означает, что "с2 = 1",
поэтому процесс 1 не может циклиться и непременно попадает в свой критический
интервал. Для случая "очередь = 2" применяется симметричное
(относительно процессов и переменных) рассуждение.
В третьей и заключительной части доказательства мы отмечаем, что остановка,
скажем процесса 1 в "остатке цикла 1", не препятствует продвижению
процесса 2: тогда справедливо соотношение "с1 = 1", и процесс 2
может входить в свой критический интервал совершенно независимо от текущего
значения переменной "очередь". Этим завершается доказательство
корректности решения Деккера. Тех читателей, которые не оценили
изобретательности этого решения, я прошу учесть, что для них уже была
подготовлена почва из тщательно подобранных мною и затем отвергнутых, как
непригодные, решений.
2.2. Обобщенная задача взаимного исключения
Задача из ╖2.1 допускает естественное обобщение: даны N
циклических процессов, каждый со своим критическим интервалом; можем ли мы так
построить их, чтобы в любой момент самое большее один процесс находился в
критическом интервале? Предположим, что в нашем распоряжении имеются те же самые
средства связи, т. е. набор переменных общего доступа. Кроме того, наше решение
должно удовлетворять тем же требованиям, а именно: остановка процесса вне его
критического интервала не может никаким образом ограничивать продвижение других
процессов, если более чем один процесс находится перед входом в свой критический
интервал, то должно быть выполнено требование о невозможности подобрать для них
такие конечные скорости, при которых решение о том, какому из них первому войти
в свой критический интервал, откладывается до бесконечности.
Чтобы записать решение на языке АЛГОЛ-60, необходимо ввести понятие массива.
В ╖2.1 мы вводили для каждого из процессов свои "с" с помощью
описания
integer cl, с2
Вместо прямого перечисления величин, мы можем использовать (в предположении,
что "N" имеет соответствующее положительное значение) следующее
описание:
integer array с[1 : N]
которое означает, что мы вводим N целых переменных, к которым
обращаются по именам с[индекс],
где "индекс" может принимать значения 1, 2, . . .,
N.
Следующей конструкцией языка АЛГОЛ-60, которую мы используем, является так
называемый оператор цикла:
for j:=l step 1 until N do оператор S;
Он дает нам возможность очень удобно задать повторение "оператора
S". В принципе эта конструкция означает, что "оператор S"
будет выполнен N раз с "j", принимающим
последовательно значения, равные 1, 2, . . ., N. (Мы добавили "в
принципе", так как с помощью оператора goto, являющегося
частью оператора S и передающего управление вне оператора
S, повторное выполнение может быть прекращено раньше.)
Наконец, нам нужна логическая операция, которая в пределах этой главы будет
обозначаться "and". Мы уже встречали условное предложение в форме:
if условие then оператор
Теперь мы будем использовать такую форму:
if условие 1 and условие 2 then оператор
которая означает, что оператор S будет выполнен, если только
"условие 1" и "условие 2" удовлетворяются оба.
(Хотелось бы еще раз подчеркнуть, что эта глава не является руководством по
программированию на АЛГОЛе и приведенные выше (нестрогие!) объяснения элементов
АЛГОЛа даются только для того, чтобы сделать излагаемый материал возможно более
самостоятельным.) С помощью только что бегло очерченных изобразительных средств
мы можем записать наше решение для фиксированного значения N
следующим образом: begin integer array b, с[0 : N],
integer очередь;
for очередь := 0 step 1 until N do
begin b[очередь] := 1; с[очередь] :=1 end;
очередь := 0;
parbegin
процесс 1: begin ............... end;
процесс 2: begin ............... end;
.
.
.
процесс N: begin ............... end;
parend
end
В первой строчке вводится два массива с N + 1 элементом каждый;
во второй вводится простая переменная "очередь". При выполнении
следующего далее цикла переменная "очередь" принимает последовательно значения
0, 1, 2, 3, ..., N, так что элементы обоих массивов получают
начальные значения, равные "1". Затем "очередь"
устанавливается в "0" (т. е. ни один из процессов, пронумерованных
от 1 до N, не поставлен в особые условия). После этого
все N процессов начинают одновременно выполняться.
2.3. Пример
В ╖2.2 мы описали взаимодействие N процессов. В приведенной
программе использована последовательность вертикальных точек между скобками
"parbegin" и "parend", что является лишь
нестрогим формализмом для изображения совокупности N
взаимодействующих последовательных процессов, при условии что N
задано заранее. Эта общая форма может быть развернута для 3, 4 или 5071
взаимодействующих процессов, но она не дает формального описания N
взаимодействующих процессов в случае, когда N является параметром,
т. е. она не справедлива для любого значения N.
Цель данного параграфа - кратко показать, как может помочь в данном случае
понятие так называемой "рекурсивной процедуры" в АЛГОЛе.
Мы видели, как с помощью описаний, следующих за "begin",
вводились и именовались простые переменные (перечислением их имен) и
упорядоченные множества переменных (описание массива). С помощью так называемого
"описания процедуры" мы можем определить и поименовать отдельное действие. Такое
действие вызывается затем использованием его имени в качестве оператора; при
этом задаются параметры, к которым требуется применить это действие.
Рассмотрим в качестве иллюстрации следующую программу:
begin integer a, b;
procedure квадрат(u, v); integer u, v;
begin u := v 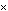 v end;
L: квадрат(а, 3); квадрат(b, а); квадрат(а, b);
end
v end;
L: квадрат(а, 3); квадрат(b, а); квадрат(а, b);
end
В первой строке программы описываются целые переменные "а" и
"b". В следующей строке начинается описание процедуры, названной
"квадрат", которая использует два параметра, являющихся простыми
целочисленными переменными (а не, скажем, массивами). Эта строка называется
"заголовком процедуры". Следующий далее оператор - так называемое "тело
процедуры" - описывает само действие с именем "квадрат": присвоить
первому параметру квадрат значения второго параметра (отметим, что скобки
"begin . . . end" в третьей строке, вообще говоря,
избыточны). Затем следует, снабженный меткой "L", первый
выполняемый оператор программы. До его выполнения значения переменных
"а" и "b" не определены, после выполнения имеем
"а = 9". После выполнения следующего оператора значение
"b" становится равным "81", после выполнения
последнего оператора получаем "а = 6561", а значение
"b" по-прежнему равно "81".
В этом примере процедура послужила по существу средством сокращения записи,
позволив избежать трехкратного включения "тела" в программу, хотя мы вполне
могли бы написать:
begin integer a, b;
L: а := 3 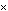 3; b := а
3; b := а 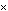 а; а := b
а; а := b 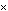 b
end
b
end
В случае более сложного, чем в этом примере, тела длина программы значительно
увеличилась бы.
Метод "подстановки вместо обращения к процедуре соответствующим образом
преобразованного тела процедуры", однако, невозможен, если процедура является
рекурсивной, т. е. сама может вызывать себя. Такая процедура действительно
расширяет выразительную силу языка программирования.
Проиллюстрируем использование рекурсивной процедуры на простом примере. Общий
наибольший делитель (ОНД) двух натуральных чисел определяется так:
- если числа равны, то ОНД равен этому общему значению;
- если числа не равны, то ОНД равен общему наибольшему делителю меньшего из
исходных чисел и их разности.
Иначе говоря, если ОНД не определяется тривиально (первый случай), то задача
его нахождения заменяется отысканием ОНД для двух чисел с меньшими значениями.
(В следующей ниже программе спецификация "value v, w;"
может быть пропущена читателем как не относящаяся по существу к обсуждаемому
вопросу; она указывает, что для тела процедуры представляют интерес лишь
числовые значения перечисленных параметров, задаваемые при обращении к
процедуре).
begin integer a;
procedure ОНД (u, v, w); value v, w; integer u, v, w;
if v = w then u := v
else
begin if v < w then ОНД (u, v, w - v)
else ОНД (u, v - w, w)
end;
ОНД (a, 12, 33)
end
(B этом примере использована более сложная форма условного оператора, а
именно:
if условие then оператор 1 else оператор 2
что означает: если "условие" удовлетворяется, то выполняется
"оператор 1", а "оператор 2" пропускается; если
"условие" не удовлетворяется, то пропускается "оператор
1", а выполняется "оператор 2".)
Читателю предоставляется проследить за последовательностью обращений к
процедуре ОНД и убедиться, что переменная "а" получает значение
"З". Необходимо также осознать, что (динамическая) схема обращений
зависит от заданных параметров, и поэтому метод подстановки из предыдущего
примера - замещение обращения к процедуре телом процедуры - привел бы здесь к
трудностям.
Теперь мы составим программу умножения матрицы на вектор, в которой:
- порядок вычисления М произведений скаляра на скаляр точно
определен (строки матрицы просматриваются слева направо);
- N строк матрицы могут обрабатываться параллельно. (Там, где
мы не хотим ограничиваться только целочисленными значениями, использован
описатель "real" вместо описателя
"integer"; кроме того, мы ввели двумерный массив, что,
вероятно, у читателя не вызовет затруднений.)
Предполагается, что перед входом в этот блок целые переменные
"М" и "N" получают положительные значения.
begin real array матрица[1 : N, 1 : M];
real array вектор[1 : M];
real array произведение[1 : N];
procedure умножстроки(k); value k; integer k;
begin if k > 0 then
parbegin
begin real s; integer j;
s := 0;
for j := 1 step 1 until M do
s := s + матрица[k, 3] 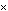 вектор[jl;
произведение[k] := s
end;
умножстроки(k - 1)
parend
end;
.
.
.
.
умножстроки(N);
.
.
end
вектор[jl;
произведение[k] := s
end;
умножстроки(k - 1)
parend
end;
.
.
.
.
умножстроки(N);
.
.
end
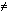 1", т. е. "очередь = 2". Но
единственный способ для переменной "очередь" получить это значение
есть присваивание "очередь := 2" в процессе 1. Так как процесс 1
выполняет это присваивание только по завершении своего критического интервала,
то процесс 2 может войти в свой критический интервал только после завершения
критического интервала 1. А критический интервал 1 действительно мог быть
выполнен, потому что начальное условие "очередь = 1" означает
одновременно "очередь
1", т. е. "очередь = 2". Но
единственный способ для переменной "очередь" получить это значение
есть присваивание "очередь := 2" в процессе 1. Так как процесс 1
выполняет это присваивание только по завершении своего критического интервала,
то процесс 2 может войти в свой критический интервал только после завершения
критического интервала 1. А критический интервал 1 действительно мог быть
выполнен, потому что начальное условие "очередь = 1" означает
одновременно "очередь 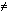 2", и значит
потенциальный цикл ожидания, помеченный в программе как L1,
первоначально бездействует. После присваивания "очередь := 2" роли
процессов меняются. {Замечание. Предполагается, что других ссылок на
переменную "очередь", кроме тех, которые явно присутствуют в
программе, не существует.)
2", и значит
потенциальный цикл ожидания, помеченный в программе как L1,
первоначально бездействует. После присваивания "очередь := 2" роли
процессов меняются. {Замечание. Предполагается, что других ссылок на
переменную "очередь", кроме тех, которые явно присутствуют в
программе, не существует.) 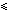 i
i 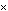 v end;
L: квадрат(а, 3); квадрат(b, а); квадрат(а, b);
end
v end;
L: квадрат(а, 3); квадрат(b, а); квадрат(а, b);
end