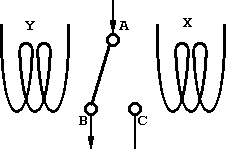
Рис.1. x<y
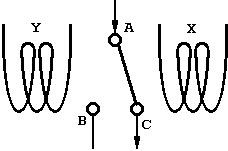
Рис.2. y<x
| Возврат на сайт | Назад | Оглавление | Вперед |
Наша проблема состоит в сущности в том, чтобы согласовать два или больше последовательных процессов. Прежде чем приступать к ней, однако, нужно совершенно отчетливо представить себе, что мы называем "последовательным процессом". Настоящий раздел посвящен этому предварительному обсуждению.
Прежде всего сравним два устройства, выполняющих одинаковую задачу, причем одно из них является не последовательным, а другое - последовательным.
Предположим, что четырем величинам, назовем их "a[1]", "a[2]", "a[3]" и "a[4]", даны некоторые значения. Наше устройство должно обработать их и "сообщить", какая из четырех величин имеет наибольшее значение. Например, в случае:
a[1] = 7, a[2] = 12, a[3] = 2, a[4] =9ответом должно быть "a[2]" (или просто "2"- индекс, указывающий на максимальный элемент).
Отметим, что в случае, когда наши величины имеют, например, значения "7, 12, 2, 12" соответственно, невозможно дать однозначный ответ, так как не существует единственного наибольшего элемента, и ответ "а[2]" был бы так же хорош (или так же плох), как и ответ "а[4]". Чтобы избежать этого, будем в дальнейшем предполагать, что никакие два из четырех значений не равны.
Замечание 1. Если бы требовалось определить максимальное значение среди заданных (а не элемент, имеющий максимальное значение), то последнее ограничение было бы излишним, так как ответом при наборе значений "7, 12, 2, 12" является "12".
Замечание 2. Наше ограничение "никакие два из четырех значений не равны" сформулировано не совсем строго, так как не определено, что подразумевается под равенством значений.
В процессах, которые мы будем рассматривать, будут сравниваться пары значений, и утверждение, что любые два значения различаются, по существу означает, что устройство сравнения всегда будет однозначно определять, какое из двух больше. Другими словами, различие между любыми двумя значениями должно быть больше, чем "разрешающая способность" устройств сравнения.
Сначала мы построим не последовательное устройство. Если предположить, что значения задаются силой тока, то можно представить устройство сравнения в виде двухпозиционного переключателя, положение которого определяется токами в катушках электромагнитов, как показано на рис.1 и 2.
 Рис.1. x<y |
 Рис.2. y<x |
Если ток y больше тока x, то сила притяжения левого электромагнита больше, чем правого, и переключатель займет левое положение (рис.1), а вход А соединится с выходом В; если ток x больше тока у (рис.2), то вход А соединится с выходом С.
Мы будем представлять такое устройство сравнения схематично в виде:
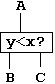
|
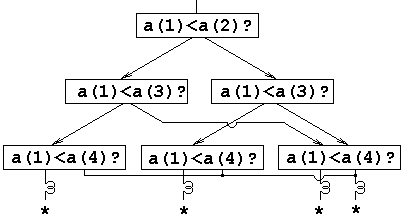 Рис.3. |
Теперь построим устройство, изображенное на рис.3. На выходе изображены четыре индикаторных лампочки, одна и только одна из которых будет загораться, указывая ответ.
На рис.4 показано положение переключателей при заданных значениях "7, 12, 2, 9". Цепи, не соединенные с входом, изображены пунктиром.
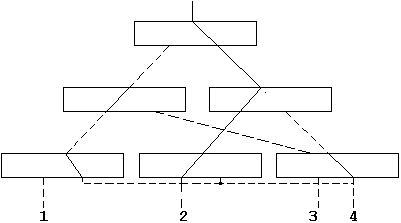 Рис.4. |
Мы обращаем внимание читателя на то, что существенны положения только трех переключателей, соединяющих вход с выходом 2; читатель может убедиться самостоятельно, что положение трех остальных переключателей действительно несущественно.
Важно также рассмотреть тот момент, когда в наше устройства (рис.3) поданы четыре тока. Очевидно, что нельзя ожидать правильного ответа, пока токи не поступят в катушки электромагнитов. Но правильный ответ нельзя получить и сразу же после подачи токов, так как переключатели должны занять правильное положение, а на это требуется определенное время. Иначе говоря, как только поданы токи (одновременно тали друг за другом), мы должны ожидать некоторое время (этот интервал времени является характеристикой машины), и только после этого на выходе появится правильный ответ: загорится соответствующая лампочка. Все, что происходит в течение этого времени ожидания, несущественно (при условии, что интервал времени достаточно большой, чтобы все переключатели заняли окончательное положение). Переключения могут начаться одновременно; точный порядок, в котором достигается окончательное положение, безразличен, и мы не будем больше обращать на это внимание.
С логической точки зрения время переключения можно рассматривать как отметку на оси времени: до этой отметки входные данные не поданы, после нее - получен ответ.
При использовании нашего устройства связь со временем отражается только в очевидном отношении "до - после", которое говорит лишь о том, что нельзя ожидать ответа, пока не поставлен надлежащим образом вопрос. Эта последовательная связь так очевидна (и фундаментальна), что она не может рассматриваться как характеристическое свойство нашего устройства. Поэтому наше устройство называется "не последовательным" в отличие от устройств (или процессов, реализуемых в них), к описанию которых мы теперь перейдем.
До сих пор мы интерпретировали диаграмму на рис.3 как схематическое изображение устройства, расположенного в пространстве. Но эту же диаграмму можно интерпретировать совершенно иным образом, если мы мысленно поставим себя на место электрона, поступающего на верхний вход и выбирающего направление движения. Во-первых, он решает, справедливо ли утверждение "а[1] < а[2]". Найдя ответ, он движется дальше. В зависимости от предыдущего ответа, он попадает в блок "a[1] < а[3]" или в блок "а[2] < а[3]", т. е. следующий шаг становится известным только после того, как получен ответ на первый вопрос. Получив ответ на вопрос, выбранный во втором уровне диаграммы, он будет знать, какой вопрос выбирать на третьей строке, и, наконец, найдя ответ на этот последний вопрос, он определит лампочку, которую нужно зажечь. Вместо того чтобы рассматривать диаграмму на рис.3 как устройство, части которого расположены в пространстве, мы интерпретировали ее как правила поведения во времени.
По отношению к первой интерпретации наиболее существенны два отличия. В первом случае все шесть устройств сравнения начинали работать одновременно, хотя в конце концов имели значение положения только трех переключателей. Во втором случае на самом деле проводилось только три сравнения (движущийся электрон должен был найти ответы на три вопроса), но ценой того, что они выполнялись поочередно, так как результат предыдущего сравнения определял, какое будет следующим. Во второй интерпретации три вопроса были заданы последовательно, друг за другом. Наличие такой упорядоченной связи является характерным свойством второй интерпретации, которая в противоположность первой называется поэтому "последовательным процессом". Сделаем два замечания.
Замечание З. Каждое из трех сравнений осуществляется за конечное время (оно называется "временем переключения", "временем решения" или "временем выполнения") и, как результат, общее время будет по меньшей мере равно сумме этих трех времен. Мы еще раз подчеркнем, что во многих исследованиях эти времена выполнения могут рассматриваться как упорядоченные отметки на оси времени, и единственное, что имеет значение с логической точки зрения, - их относительный порядок.
Замечание 4. Эти две интерпретации (назовем их "одновременные сравнения" и "последовательные сравнения") являются только крайними случаями. Можно снова ограничиться выполнением трех сравнений, два из которых могут быть осуществлены независимо друг от друга, т. е. одновременно, а третье производится только после завершения двух предыдущих. Такое устройство можно представить с помощью блока, в котором помещаются два вопроса, и который имеет четыре возможных результирующих выхода (рис.5). Общее время будет равно по меньшей мере сумме времен выполнения сравнений. Процесс принадлежит к первому виду в том смысле, что первые два сравнения могут быть выполнены одновременно, и вместе с тем он является последовательным, так как третье сравнение можно выбрать со второго уровня диаграммы только после завершения двух первых сравнений.
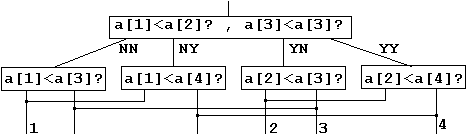 Рис.5. |
Вернемся к случаю чисто последовательной интерпретации. Мы можем воспользоваться этой интерпретацией, чтобы сделать описание "правил поведения" более компактным. Идея состоит в том, что два вопроса на втором уровне (только один из которых будет фактически задан) очень схожи, и вообще: вопросы на одном и том же уровне различаются только значением индекса левого операнда в операции сравнения. А нельзя ли изобразить вопросы одного уровня на рис.3 в виде единственного вопроса?
Сделать это можно, но это означает, что изменяющаяся вдоль уровня часть вопроса - значение индекса левого операнда, - должна рассматриваться как параметр, назначение которого состоит в определении того, какой из вопросов имеется в виду, когда очередь доходит до этого уровня. Очевидно, что значение этого параметра должно быть определено предыдущей историей процесса.
Такие параметры, в которых выражена прошлая история для использования в будущем, называются "переменными". Чтобы присвоить новое значение переменной, мы будем использовать так называемую операцию присваивания ":=" (читается: "становится") - ориентированный знак равенства, который определяет значение левой части в терминах значения правой части.
Мы надеемся, что сказанного выше достаточно, чтобы распознать в диаграмме на рис. 6 набор "правил поведения". Наша переменная называется "i". Читателя может удивить, почему первый вопрос, который всегда имеет вид "a[1] < a[2]?", не записан именно так, но после небольшого размышления он это поймет.
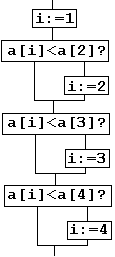 Рис.6. |
Если мы будем следовать правилам на рис. 6, спускаясь сверху вниз, то полученное конечное значение i определит максимальное значение a[i].
Переход от схемы на рис.3 к схеме на рис.6 носит принципиальный характер, так как в последнем "правила поведения" можно интерпретировать только последовательно. Это происходит вследствие введения переменной "i": когда для сравнения используются только величины a[1], a[2], a[3] и a[4], вопрос "a[i] < a[2]?" будет бессмысленным, если неизвестно, для какого значения "i" это сравнение нужно выполнить.
Замечание 5. Несколько неудачно, что на профессиональном жаргоне величина, подобная "i", называется переменной, так как обычно в математике понятие переменной совершенно не зависит от времени. Например, время никак не влияет на "x" в соотношении
sin (2если эта переменная вообще обозначает значение, то она обозначает "любое значение".х) = 2
sin (x)
cos (x);
Однако всякий раз, когда переменная используется в последовательном процессе (например, "i" в конструкции "a[i]"), она обозначает совершенно конкретное значение, а именно последнее значение, присвоенное этой переменной, и ничего больше. Пока переменной не присвоено новое значение, ее значение остается постоянным.
Замечание 6. Могут спросить, допустимо ли вводить переменную, не указывая, например, область ее значений, содержащую все будущие фактические значения переменной. Мы не будем здесь заниматься обсуждением этого вопроса.
Теперь мы подвергнем нашу схему новому преобразованию. В схеме на рис.3 мы "свернули" уровни, а сейчас мы собираемся свернуть схему на рис.6 по вертикали, используя ее "повторяющийся" характер. Эта операция может быть выполнена посредством введения новой переменной "j".
Результат преобразования весьма значителен, так как тот факт, что первоначальная задача была поставлена для четырех значений, больше не отражается на "топологии" правил поведения: на рис.7 мы обнаруживаем только упомянутое число "4". Вводя еще одну переменную, скажем "n", и заменяя "4" на "n", мы немедленно получаем правила для отыскания максимального среди n элементов a[1], a[2] , . . ., a[n]. Перед практическим применением этих правил переменной "n" необходимо лишь дать нужное значение.
Итак, мы не только располагаем правилами, которые должны интерпретироваться последовательно (это было уже в схеме на рис.6), но теперь мы создали единый механизм для нахождения максимального значения среди любого числа данных элементов, тогда как наше первоначальное не последовательное устройство могло быть построено только для наперед заданного числа элементов. Мы представили наши сравнения во времени, а не в пространстве, и если сравнивать оба метода, то последовательное устройство как бы "саморасширяется", когда возникает необходимость (на схеме рис.3 для не последовательного устройства это эквивалентно добавлению соответствующих блоков).
Техническим термином для того, что мы назвали "правила поведения", является алгоритм или программа. (Не принято говорить "последовательная программа", хотя такое название было бы абсолютно правильным.) Устройство, которое может следовать этим правилам, "выполнять такую программу", называется "универсальной последовательной вычислительной машиной", или, коротко, "вычислительной машиной". То, что происходит при выполнении такой программы, называется "последовательным процессом".
Существует общепринятый метод записи алгоритмов без использования рисунков, подобных приведенным выше, например, язык АЛГОЛ-60 ("ALGOL" является сокращением от Algorithmic Language - алгоритмический язык). Для детального знакомства с языком АЛГОЛ-60 читатель может воспользоваться соответствующей литературой. В дальнейшем, когда это будет удобно, мы будем использовать АЛГОЛ-60.
С целью иллюстрации мы запишем алгоритм на рис.7 (с "n" вместо "4") в виде последовательности операторов АЛГОЛа:
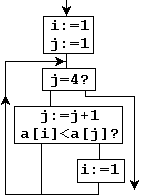 Рис.7. |
i:= 1; j:= 1;
повторить: if j 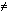 n then
begin j := j + 1;
if a[il<a[]] then i := j;
goto повторить;
end
n then
begin j := j + 1;
if a[il<a[]] then i := j;
goto повторить;
end
Первые два оператора: "i:=1; j:=l" очевидны. Затем следует
"повторить", так называемая метка, используемая, чтобы отметить данное место в
программе. Затем следует так называемое условное предложение "if j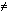 n then". Если выраженное им условие
удовлетворяется, то будет выполняться следующий оператор, в противном случае
следующий оператор будет пропущен. (Другой пример условного оператора можно
найти двумя строками ниже.) Если участок программы, который может быть пропущен,
представляет собой последовательность из более чем одного оператора, то эта
последовательность заключается в так называемые операторные скобки
"begin" и "end", и тем самым
превращается в единый оператор, когда речь идет о его окружении. (Это полностью
аналогично действию скобок в алгебраической формуле, такой как "а
n then". Если выраженное им условие
удовлетворяется, то будет выполняться следующий оператор, в противном случае
следующий оператор будет пропущен. (Другой пример условного оператора можно
найти двумя строками ниже.) Если участок программы, который может быть пропущен,
представляет собой последовательность из более чем одного оператора, то эта
последовательность заключается в так называемые операторные скобки
"begin" и "end", и тем самым
превращается в единый оператор, когда речь идет о его окружении. (Это полностью
аналогично действию скобок в алгебраической формуле, такой как "а 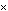 (b + с)", где пара скобок указывает, что все
выражение, заключенное в них, является сомножителем.) Последний оператор
"goto повторить" означает, что процесс должен быть продолжен
с точки, помеченной этой меткой; он делает в точности то же, что и направленная
вверх стрелка на рис.7.
(b + с)", где пара скобок указывает, что все
выражение, заключенное в них, является сомножителем.) Последний оператор
"goto повторить" означает, что процесс должен быть продолжен
с точки, помеченной этой меткой; он делает в точности то же, что и направленная
вверх стрелка на рис.7.
| Возврат на сайт | Назад | Оглавление | Вперед |