6.2. Применение алгоритма банкира
Этот пример также связан с флоринами. (Каждому флорину можно поставить в
соответствие магнитную ленту; тогда заем флорина будет означать разрешение на
использование одной из лент.)
Предположим, что клиенты пронумерованы от 1 до N, и
что флорины пронумерованы от 1 до M. С каждым клиентом
связывается переменная "номер флорина", значение которой после
очередной выдачи флорина клиенту определяет номер только что выделенного
флорина. В свою очередь с каждым флорином связана переменная "номер
клиента", значение которой указывает клиента, которому выдан этот флорин.
Каждый клиент имеет переменную состояния "клиентпер" -
переменная клиента; при этом "клиентпер = 1" означает "Я хочу
получить заем" (иначе, "клиентпер = 0"). Каждый флорин имеет
переменную состояния "флоринпер"; при этом "флоринпер =
1" означает "Я нахожусь среди наличного капитала". С каждым клиентом и
каждым флорином связаны двоичные семафоры "клиентсем" и
"флоринсем" соответственно, которые будут использоваться обычным
образом.
Предполагаем, что каждый флорин выдается и возвращается на основании указаний
клиента, но клиент не имеет возможности возвратить занятый флорин мгновенно.
После того как клиент заявил, что флорин ему больше не нужен, последний не
становится немедленно доступным для последующего использования. То есть клиент
как будто говорит взятому им флорину: "Ступай обратно к банкиру". Фактический
возврат флорина заканчивается после того, как тот действительно присоединится к
наличному капиталу банкира: об этом флорин будет сообщать клиенту с помощью
общего семафора клиента "возвращенные флорины".
P-операция над этим семафором должна предостеречь клиента от
неумышленного превышения своего кредита в банке. Перед каждым запросом флорина
клиент выполнит P-операцию над семафором "возвращенные
флорины"; начальное значение переменной "возвращенные
флорины" полагается равным "потребность".
Предполагаем, что целочисленные константы "N" и "M"
(равная капиталу) и массив целочисленных констант "потребность"
описаны и определены во внешних по отношению к данной программе блоках.
Значение булевой процедуры "попытка выдать флорин клиенту"
говорит о том, удовлетворен ли задержанный запрос на флорин. В программе для
флорина используется тот факт, что возврат флорина может теперь привести к
удовлетворению единственного задержанного запроса на флорин. (Если банкир
распоряжается услугами более чем одного вида, то последнее свойство уже не будет
выполняться. Тогда выход из цикла на оператор с меткой "выход" в
конце программы для флорина недопустим.)
begin integer array заем, требование, клинтсем, клиентпер,
номер флорина, возвращенные флорины[1 : N],
флоринсем, флоринпер, номер клиента[1 : М];
integer взаимискл, наличные, k;
Boolean procedure попытка выдать флорин клиенту(j);
value j; integer j;
begin if клиентпер[j] = 1 then
begin integer i, свободные деньги;
Boolean array завершение под сомнением[1 : N];
свободные деньги := наличные - 1;
требование[j] := требование[j] - 1; заем[j] := заем[j] + 1;
for i := 1 step 1 until N do завершение под сомнением[i] := true;
L0: for i := 1 step 1 until N do
begin if завершение под сомнением[i] and
требование[i] 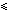 свободные деньги then
begin if i
свободные деньги then
begin if i 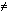 j then
begin завершение под сомнением[i] := false;
свободные деньги := свободные деньги + заем[i];
goto L0
end
else
begin comment Можно реализовать и более сложный способ
выбора свободного флорина, чем предлагаемый здесь;
i := 0;
L1: i := i + 1; if флоринпер[i] = 0 then goto L1;
номер флорина[j] := i;
номер клиента[i] := j;
клиентпер[j] = 0;
флоринпер[i] := 0;
наличные := наличные - 1;
попытка выдать флорин клиенту := true;
V(клиентсем[i]);
V(флоринсем[i]); goto L2
end
end
end;
требование[j] := требование[j] + 1;
зaeм[j] := зaeм[j] - 1
end;
попытка выдать флорин клиенту := false;
L2: end процедуры;
взаимискл := 1; наличные := M;
for k := 1 step 1 until N do
begin заем[k] := 0; клиентсем[k] := 0; клиентпер[k] := 0;
требование[k] := потребность[k];
возвращенные флорины[k] := потребность[k]
end;
for k := 1 step 1 until M do
begin флоринсем[k] := 0; флоринпер[k] := 1 end;
parbegin
клиент 1: begin. ........... end;
.
.
.
клиент N: begin. ........... end;
флорин 1: begin. ........... end;
.
.
.
флорин M: begin. ........... end;
parend
end
j then
begin завершение под сомнением[i] := false;
свободные деньги := свободные деньги + заем[i];
goto L0
end
else
begin comment Можно реализовать и более сложный способ
выбора свободного флорина, чем предлагаемый здесь;
i := 0;
L1: i := i + 1; if флоринпер[i] = 0 then goto L1;
номер флорина[j] := i;
номер клиента[i] := j;
клиентпер[j] = 0;
флоринпер[i] := 0;
наличные := наличные - 1;
попытка выдать флорин клиенту := true;
V(клиентсем[i]);
V(флоринсем[i]); goto L2
end
end
end;
требование[j] := требование[j] + 1;
зaeм[j] := зaeм[j] - 1
end;
попытка выдать флорин клиенту := false;
L2: end процедуры;
взаимискл := 1; наличные := M;
for k := 1 step 1 until N do
begin заем[k] := 0; клиентсем[k] := 0; клиентпер[k] := 0;
требование[k] := потребность[k];
возвращенные флорины[k] := потребность[k]
end;
for k := 1 step 1 until M do
begin флоринсем[k] := 0; флоринпер[k] := 1 end;
parbegin
клиент 1: begin. ........... end;
.
.
.
клиент N: begin. ........... end;
флорин 1: begin. ........... end;
.
.
.
флорин M: begin. ........... end;
parend
end
У клиента "n" запрос нового флорина описывается следующей
последовательностью операторов:
P(возвращенные флорины[n]);
P(взаимискл);
клиентпер[n] := 1;
попытка выдать флорин клиенту(n)
V(взаимискл);
P(клиентсем[n]);
после завершения последнего оператора значение переменной "номер
флорина [n]" определяет только что выданный флорин; клиент может
использовать его, но обязан возвратить его в надлежащее время банкиру.
Структура программы для флорина следующая:
флорин m:
begin integer h;
начало: P(флоринсем[m]);
comment Теперь "номер клиента [m]" указывает клиента, которому
выдан данный флорин. Флорин может обслуживать клиента до тех пор,
пока не закончит задачу, поставленную перед ним в течение этого
заема. Чтобы возвратиться к наличному капиталу, флорин поступает
следующим образом:
P(взаимискл);
требование[номер клиента[m]] := требование[номер клиента [m]] + 1;
заем[номер клиента[m]] := заем[номер клиента[m]] - 1;
флоринпер[m] := 1; наличные := наличные + 1;
V(возвращенные флорины[номер клиента[m]]);
for h := 1 step 1 until N do
begin if попытка выдать флорин клиенту(h) then
goto выход
end;
выход: V(взаимискл);
goto начало
end
Замечание. Грубо говоря, успешный заем флорина может иметь место
только при удовлетворении двух условий: флорин должен быть затребован и флорин
должен быть доступен. В этой программе механизм общих переменных
"клиентпер" и "клиентсем" используется также
(клиентом) в случае, когда затребованный флорин немедленно предоставлен; подобно
этому, механизм общих переменных "флоринпер" и
"флоринсем" используется также (флорином) в случае, если после
возвращения его в наличный капитал он может немедленно быть выдан снова
ожидающему клиенту. Этот метод программирования был предложен Лайтмансом и
Вуурхоеве, и я упоминаю о нем потому, что в случае более сложных правил
взаимодействия он приводит к упрощениям, которые оказываются крайне полезными.
Основной причиной достижения большей простоты является то, что динамическое
движение через топологическую структуру программы больше не проводит различие
между фактической задержкой и потенциальной, точно так же как в случае самой
P-операции.
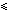 свободные деньги then
begin завершение под сомнением[i] := false;
свободные деньги := свободные деньги + заем[i];
goto L
end
end;
if свободные деньги = капитал
then безопасно := true
else безопасно := false
свободные деньги then
begin завершение под сомнением[i] := false;
свободные деньги := свободные деньги + заем[i];
goto L
end
end;
if свободные деньги = капитал
then безопасно := true
else безопасно := false
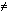 j then
begin завершение под сомнением[i] := false;
свободные деньги := свободные деньги + заем[i];
goto L0
end
else
begin comment Можно реализовать и более сложный способ
выбора свободного флорина, чем предлагаемый здесь;
i := 0;
L1: i := i + 1; if флоринпер[i] = 0 then goto L1;
номер флорина[j] := i;
номер клиента[i] := j;
клиентпер[j] = 0;
флоринпер[i] := 0;
наличные := наличные - 1;
попытка выдать флорин клиенту := true;
V(клиентсем[i]);
V(флоринсем[i]); goto L2
end
end
end;
требование[j] := требование[j] + 1;
зaeм[j] := зaeм[j] - 1
end;
попытка выдать флорин клиенту := false;
L2: end процедуры;
взаимискл := 1; наличные := M;
for k := 1 step 1 until N do
begin заем[k] := 0; клиентсем[k] := 0; клиентпер[k] := 0;
требование[k] := потребность[k];
возвращенные флорины[k] := потребность[k]
end;
for k := 1 step 1 until M do
begin флоринсем[k] := 0; флоринпер[k] := 1 end;
parbegin
клиент 1: begin. ........... end;
.
.
.
клиент N: begin. ........... end;
флорин 1: begin. ........... end;
.
.
.
флорин M: begin. ........... end;
parend
end
j then
begin завершение под сомнением[i] := false;
свободные деньги := свободные деньги + заем[i];
goto L0
end
else
begin comment Можно реализовать и более сложный способ
выбора свободного флорина, чем предлагаемый здесь;
i := 0;
L1: i := i + 1; if флоринпер[i] = 0 then goto L1;
номер флорина[j] := i;
номер клиента[i] := j;
клиентпер[j] = 0;
флоринпер[i] := 0;
наличные := наличные - 1;
попытка выдать флорин клиенту := true;
V(клиентсем[i]);
V(флоринсем[i]); goto L2
end
end
end;
требование[j] := требование[j] + 1;
зaeм[j] := зaeм[j] - 1
end;
попытка выдать флорин клиенту := false;
L2: end процедуры;
взаимискл := 1; наличные := M;
for k := 1 step 1 until N do
begin заем[k] := 0; клиентсем[k] := 0; клиентпер[k] := 0;
требование[k] := потребность[k];
возвращенные флорины[k] := потребность[k]
end;
for k := 1 step 1 until M do
begin флоринсем[k] := 0; флоринпер[k] := 1 end;
parbegin
клиент 1: begin. ........... end;
.
.
.
клиент N: begin. ........... end;
флорин 1: begin. ........... end;
.
.
.
флорин M: begin. ........... end;
parend
end